Beginner’s Guide to Comparing Six Machine Learning Models for Energy Consumption Forecasting: A Five-Month Study (Part 1)
Explore how to predict time series energy consumption data with Machine Learning.
Over the last five months, I have compared 6 different machine learning models to predict energy consumption data over 48 hours. In addition to simpler statistical machine learning models (SARIMAX, Exponential Smoothing, TBATS), I have also applied 2 deep learning models (LSTM architecture and Transformer architecture) to my energy consumption data (data set over 3 years). In addition to the energy consumption data, I also provided the models with meteorological data for the forecast. The article shows you how to get started as a beginner in the world of machine learning by applying data to different models.
In the article, you learn what is special about the prediction of time series data, which research gaps exist in this area and which models I used. In one of my previous articles, you will find a Beginner’s Guide to Predicting Time Series Data with Python.
Predicting Time Series Data
Time series data are data sets that consist of time stamps and associated information. We encounter such data all the time in the world: Stock prices, weather data, products sold at certain times, or energy consumption data.
In many forecasting tasks, training and test data sets are often split randomly in a ratio of 80–20. With time series data, however, this division must be chronological: For example, you use all but the last 2 weeks of data for the training data set, while you build the test data set with the data from the last 2 weeks. This allows you to compare the predictions for these two weeks with the actual data.
Pro tip: If you want to further improve the generalisability of the results, you should also use a validation data set.
Time series data, such as energy consumption data, often show trends and seasonalities.
Simply put, a model analyses either the trend or the seasonality of the data:
Additiv: 𝐷(𝑡)=𝑤1⋅𝑇(𝑡)+𝑤2⋅𝑆(𝑡)D(t)=w1⋅T(t)+w2⋅S(t)Multiplikativ: 𝐷(𝑡)=𝑤1⋅𝑇(𝑡)⋅𝑤2⋅𝑆(𝑡)D(t)=w1⋅T(t)⋅w2⋅S(t)Goals of the Study and Identified Research Gaps
The central problem of the study was the utilization of real-time data from smart meters in the energy supply sector in Switzerland. Despite large volumes of data, there are challenges in utilizing this data in real-time due to data protection regulations and the latency of IT systems. This can lead to data gaps, which makes it difficult to accurately assess current energy consumption. I conducted the study as part of a business informatics bachelor’s program to investigate the suitability of various machine learning models for predicting energy consumption.
I have identified 7 research gaps:
Integration and Analysis of Real-Time Data: It’s still a challenge to integrate real-time data from smart meters and use it to accurately predict energy consumption.
Methodology: Most studies use one approach and compare it to another model or systematically review the research literature. Few studies comprehensively compare the performance and efficiency of different modern models for time series data.
Forecast Period: Most studies focus on short-term energy consumption forecasts, but not on long-term forecasts.
Balancing of Energy Flows: Most studies use energy consumption data but do not consider energy production by households.
Influencing Factors: Few studies consider meteorological influences in addition to the data.
Multidimensional Evaluation Criteria: Most studies focus on prediction accuracy. Only a few consider the resources required and the complexity of the model.
Real Application Scenarios: No study found tests the models with data from transformer stations in real-world scenarios to evaluate their practical suitability.
With my study I could contribute to 1., 2. 6. and partly to 5. and 7.
Models used to predict Energy Consumption Time Series Data
Before I applied the models, I performed an Exploratory Data Analysis (EDA) to understand the data sets. You can find the key steps for performing an EDA on time series data in my previous article, Mastering Time Series Data: 9 Essential Steps for Beginners before applying Machine Learning in Python. The regression analysis served as a baseline to identify potential improvements through more complex algorithms. I also used SARIMAX, TBATS and Triple Exponential Smoothing. You can find an explanation of these 4 models in the article Beginner’s Guide to Predicting Time Series Data with Python. Besides the statistical machine learning models, I applied advanced LSTM and Transformer architectures. I also tried to improve the model accuracy with additional variables from meteorological data.
(S)ARIMA(X) stands for (Seasonal) Autoregressive Integrated Moving Averages (with exogenous variables). The method originates from the well-known ARIMA family, but also takes into account the seasonality in the data and allows for exogenous variables. TBATS stands for Trigonometric Seasonality, Box-Cox Transformation, ARMA Error, Trend and Seasonal Components. The model was developed specifically for dealing with complex seasonal patterns. Exponential Smoothing gives greater weight to more recent observations than to older observations.
Long Short-Term Memory Network (LSTM) for the prediction of energy consumption data
LSTMs are recurrent neural network architectures that were originally used in image and speech processing. More recently, however, they have also been used to predict time series data. LSTMs were developed to solve the problem of gradient descent in traditional neural networks when processing long sequences of data. LSTMs can retain information over many time steps.
How the LSTM architecture is structured

The input layer contains the input features. In this study, I used 10 variables that were passed to the LSTM layer in sequences of 192 time points each (4 intervals * 48h = 192). The LSTM layer processes this data to recognize long-term dependencies and extract relevant information. The cell state carries relevant information through the sequence. The Forget Gate decides which information should be forgotten and which should be retained. The input gate evaluates what new information is added, with a sigmoid activation function and a tanh layer generating new values. The output gate uses the current cell state and the previous hidden state to calculate the next hidden state. After the LSTM layer, the data moves into the dense layer, which reduces the dimension from the size of the hidden layer to the final output size (in this study from 100 to 1).
Transformer for the Prediction of Energy Consumption Data
The concept of transformer models became known in 2017 with the research paper ‘Attention is All You Need’. Most people are familiar with their use of natural language processing. The big difference to earlier models is that Transformers process sequences all at once and recognize relationships between any points in a sequence through self-attention. This helps to better recognize complex patterns and shortens training times.
In time series predictions, usually only the encoder part is used to predict the next values. Since the architecture processes sequences all at once, positional encoding is important. It helps the model to understand the position of the individual data in the sequence and to model the sequence, even if they are processed simultaneously.
How the Transformer architecture is structured
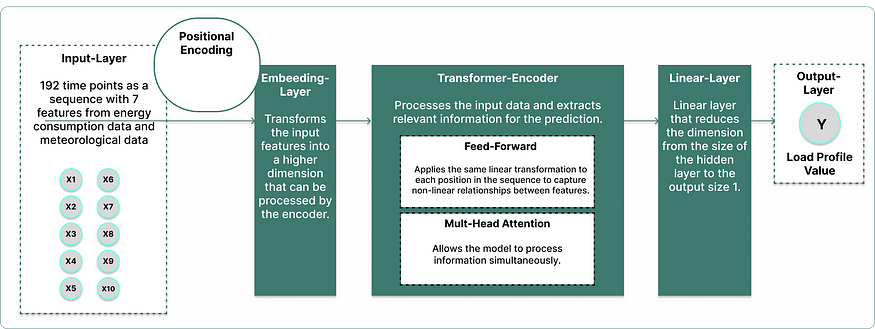
The input layer contains the input features (10 variables in this study) that are passed to the encoder. Positional encoding is added to each input vector to preserve the order of the time points. The embedding layer transforms the input features into a higher dimension for processing by the encoder. The transformer encoder extracts and processes the relevant information using multi-head attention, which analyses different aspects of the input data simultaneously and recognizes relationships. Subsequently, the feed-forward layer transforms each position of the sequence independently through linear transformations and activations. These mechanisms improve the model’s ability to recognize the immediate and long-term relevance of data points. Finally, the linear layer reduces the dimension of the data to the final output size (in this study from 100 to 1).
Where is the best place to continue learning?
Conclusion
We encounter time series data everywhere. It is therefore important to find methods to optimize the prediction of this data. In the second article in this series, I present the results of the study. Spoiler alert: The two deep learning methods produced the best results.
References



